|
PROPOSITIO XIII.
Si duae portiones de conoide paraboles, altera plano recto, altera obliquo ad axem abscindantur, fuerintque earum axes aequales; et ipsas portiones aequales esse necesse est. Item et conos, qui easdem cum portionibus bases, eosdemque habent axes inter se aequales esse.
Quod quinta praecedentis libelli de planis sectionibus, triangulisque demonstravit in parabola: haec de solidis conoidis parabolici portionibus, conisque demonstrat. Assumemus igitur quintae praedictae descriptionem, in qua sit conoides solidum a parabola ABC circa axem BG circumlata descriptum; ductoque plano recto ad axem, ac secando faciente circulum per 17. praemissi, cuius diameter sit CGH, centrumque G portio solida abscindatur CBH; conusque intelligatur super eumdem circulum, eumdemque axem, qui sit CBH. Item ducto plano obliquo ad axem, ac secando faciente ellipsim per 23. praemissi cuius diameter sit AFE, centrumque F; portio item solida abscindatur ADE; itaut eius axis DF aequidistans ipsi BG, sit [S:257] eidem BG aequalis: conus item intelligatur super eamdem ellipsim AE, et circa eumdem axem DF.
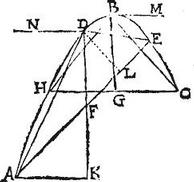Demonstrandum est igitur, quod portiones duae conoides CBH, ADE sunt aequales, quodque coni CBH, ADE sunt inter se aequales. Ducatur enim DL perpendicularis ad AE; et AK perpendicularis ad DF productam; eritque per praecedentem AK aequalis minori semidiametro ellipsis AE, et per 5. praecedentis aequalis ipsi GH semidiametro circuli CH: quare per 3. corollarium nonae praemissi libelli quando ellipsis AE minor diameter est aequalis diametro circuli CGH erit ellipsis AE ad circulum CH sicut diameter AE ad diametrum CH; et sicut semidiameter AF ad semidiametrum GH; hoc est sicut FA ad AK: et propter similitudinem triangulorum FAK, FDL, sicut FD ad DL; hoc est sicut BG ad DL (quoniam FD, BG aequales per hypothesim:) itaque conorum ADE, CBH bases sunt altitudinibus reciprocae: aequales ergo sunt coni ADE, CBH per 14. praecedentis libelli. verum per 10. huius portio conoidis CBH sexquialtera est ad conum CBH: et per 11. huius portio conoidis ADE sexquialtera est ad conum ADE; (quandoquidem portiones eamdem singulae basim, eumdemque axim cum conis sortiuntur:) igitur, et portiones ADE, CBH ex solido conoide parabolico abscissae sunt aequales: sicut iam proponitur demonstrandum.
|