PROPOSITIO VI.
Circulorum peripheriae sunt diametris proportionales.
Sunto enim duo circuli AB, GD, quorum diametri AB, GD: aio quod diameter AB ad diametrum GD, sicut peripheria AB ad peripheriam GD. Sit enim sicut diameter AB ad diametrum GD, sic iam peripheria AB ad peripheriam EZ; et erit peripheria EZ aequalis peripheriae GD. Secus enim erit minor, aut maior, si minor sit ipsi GD concentrica, et per 13.12. inscribatur peripheriae GD polygonium aequilaterum, quod peripheriam EZ non tangat; et aliud ipsi simile intra peripheriam AB: eritque propter figurarum similitudinem, sicut diameter AB ad diametrum GD, sic perimeter figurae AB ad perimetrum figurae GD. Quare sicut perimeter figurae AB ad perimetrum figurae GD: sic erit peripheria AB ad peripheriam EZ: maior autem perimeter figurae GD quam peripheria EZ, nimirum continens contento: ergo per 14.5. maior erit perimeter figurae AB quam peripheria AB: comprehensum comprehendente; quod est impossibile.
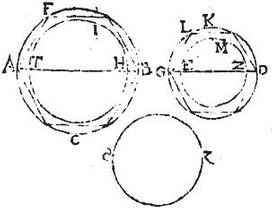
Si autem peripheria EZ sit maior quam peripheria GD; tunc conversim erit, peripheria EZ ad peripheriam AB, sicut diameter GD ad diametrum AB, et sic sit iam peripheria GD ad peripheriam TH. eritque per 14.5. minor peripheria TH quam peripheria AB: itaque erit sicut diameter GD ad diametrum AB; sic nunc peripheria GD ad peripheriam TH minorem peripheria ipsius diametri AB: quod ducit ad primum impossibile. Quamobrem non erit peripheria EZ maior quam peripheria GD: fuitque ostensum quod nec minor: omnino igitur erit ei aequalis; fuit autem peripheria AB ad peripheriam EZ, sicut diameter AB ad diametrum GD: ergo et peripheria AB ad peripheriam GD, erit item sicut diameter AB ad diametrum GD, quod erat demonstrandum. Manifestum est ergo quod sicut est diameter propositi circuli ad aggregatum ex diametris quorumcumque circulorum; sic est peripheria propositi circuli ad aggregatum ex peripheriis omnium illorum circulorum, hoc enim sequitur ex praemissa, et 13.5..
Quare si diameter propositi circuli sit aequalis aggregato ex diametris quotcumque circulorum; et peripheria propositi circuli aequalis erit aggregato ex peripheriis omnium illorum circulorum.
Item quod fit ex diametro primi circuli in peripheriam secundi aequale est ei, quod fit ex diametro secundi in peripheriam primi; idemque de semidiametris, ac peripheriis dicendum. Id enim sequitur ex praemissa, et 15.6.
Denique si trium circulorum diametri sint continue proportionales: tunc quoniam et eorum peripheriae sunt in eadem ratione proportionales, estque ob id, sicut semidiameter primi ad semidiametrum secundi, sic semiperipheria secundi ad semiperi[S:47]pheriam tertii: propterea per 15.6. erit, quod fit ex diametro primi in semiperipheriam tertii, aequale ei, quod fit ex semidiametro secundi in semiperipheriam ipsius secundi; et perinde aequale ipsi circulo secundo. Quin ex semidiametro in semiperipheriam producitur area circuli.
ALIA DEMONSTRATIO EIUSDEM SEXTAE.
Sunto duo circuli AB, GD, quorum diametri AB, GD. Aio quod peripheria AB ad peripheriam GD est sicut diameter AB ad diametrum GD: nam si sic non fuerit, erit sicut diameter AB ad diametrum GD, sic peripheria AB ad aliquam peripheriam minorem, maioremve peripheria GD. Sit ergo primum sicut diameter AB ad diametrum GD, sic peripheria AB ad peripheriam EZ minorem peripheria GD, et ei concentricam, et per 13.12. inscribatur circulo GD polygonium aequalium laterum non tangentium circulum EZ quod sit polygonium GD, et simile ipsi circulo AB inscribatur, eritque propter polygoniorum similitudinem, perimeter polygonii AB ad perimetrum polygonii GD, sicut diameter AB ad diametrum GD, et ideo sicut peripheria circuli GB ad peripheriam circuli EZ: et permutatim, erit sicut peripheria circuli AB ad perimetrum polygonii AB, sic peripheria circuli EZ ad perimetrum polygonii GD: sed peripheria circuli AB maior est perimetro polygonii AB: ergo peripheria circuli EZ maior est perimetro polygonii GD: inclusa includente, quod est impossibile.
Sit deinde sicut diameter AB ad diametrum GD, sic peripheria AB ad peripheriam HT maiorem peripheria GD, eritque conversim, sicut diameter GD ad diametrum AB, sicut peripheria HT ad peripheriam AB, et sic sit peripheria GD ad quampiam peripheriam EZ, eritque permutatim, sicut peripheria HT ad peripheriam GD, sic peripheria AB ad peripheriam EZ, maior autem peripheria HT quam peripheria GD: ergo, et maior peripheria AB, quam peripheria EZ. Quare fiet sicut diameter GD ad diametrum AB, sic peripheria GD ad peripheriam EZ minorem peripheria AB. Unde sequitur idem impossibile, quod prius. Itaque ratio diametri AB ad diametrum GD non est sicut peripheria AB ad peripheriam aliquam maiorem, minoremve peripheria GD: erit ergo sicut ipsa peripheria AB ad peripheriam GD, quod erat demonstrandum; quamquam idem in quinta libelli de dimensione circuli abstractive demonstratur.
COROLLARIUM.
Manifestum est ergo quod sicut est diameter dati circuli ad aggregatum diametrorum quotcunque circulorum, sic peripheria dati circuli ad aggregatum ex peripheriis omnium illorum circulorum: hoc enim patet ex praemissa, et 13.5. quapropter si diameter sit aequalis aggregato diametrorum, peripheria erit aequalis aggregato peripheriarum.
COROLLARIUM.
Item quod fit ex diametro circuli in peripheriam alterius circuli, aequum ei, quod ex diametro huius in peripheriam illius: hoc patet ex praesenti, et 15.6.