50^a Eisdem existentibus: si a centro sectionis coincidat quaedam tangenti aequidistans ductae lineae per tactum et unum punctorum comparatorum, aequalis erit dimidio axis.

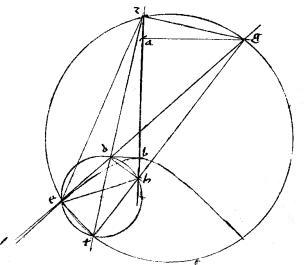
308 Sint enim eadem, quae prius. // Et centrum t. // Et coniungatur ez. // Ipsae autem ba dg concurrant ad c. // Et ipsi ez aequidistans ducatur tl. // Dico iam quod tl aequalis est ipsi tb. // Coniungantur enim eh al lh lb. // Sitque ipsi ez aequidistans hm. // Quoniam igitur az hb aequales: et ta tb aequales ideo et zt th aequales quare et el lm aequales. 309 // Et, quoniam per 48^am huius, anguli gez deh sunt aequales. // Et propter aequidistantiam linearum, anguli gez emh aequales. // Ideo ipsi emh deh anguli aequales. // Quare, per 6^am primi Euclidis ipsae lineae eh hm aequales. // Fuere autem el lm aequales. // Et hl communis. // Ergo aequilatera invicem cum sint hel hml. // Erunt, [A:93v] per 8^am primi Euclidis et invicem aequiangula. 310 // Quare anguli hle hlm aequales et hl kathetus ad dg. // Igitur, per praecedentem, angulus alb rectus. // Quam ob rem, circulus super centro t diametroque ab descriptus ibit per l punctum. // Unde ex diffinitione circuli tl aequalis est ipsi tb. // Quod fuit demonstrandum.

Additio

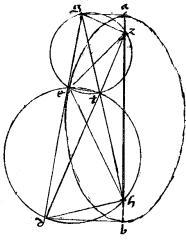
311 Quod si e punctum tactus sit apud extremum axis minoris⁴¹⁵, qui sit te atque ideo tunc ipsae ba dg sint aequidistantes; in ellipsi; adhuc per eadem ostendetur tl aequalis ipsi tb. // Quod et hoc pacto demonstrabitur. Nam cum zt th⁴¹⁶ sint aequales azh aequale⁴¹⁷ duplo ipsius azc.

// Per 3am autem 2i Euclidis azh az simul aequalia haz.

// 312 Ergo et azt az simul aequalia eidem haz hoc 418 azb

quod per hypothesim est 1/4 speciei ad ab et per corollarium 13^ae vel 15^ae primi Conicorum, aequale te.

// Sed per 4am secundi Euclidis at aequale est tz za azt .

313 // Igitur at aequale zt te sed zt te

per penultimam primi Euclidis aequalia ze. // Ergo et ze aequale [A:94r] at. // Quare et ze aequalis ipsi at. // Verum cum parallelogrammum sit ipsum zelt iam tl aequalis est ze. // Et ideo tl aequalis erit ipsi at hoc est ipsi tb dimidio axis. // Sicut proponitur demonstrandum.